Legendre
January 31, 2024, 2:34pm
22
Fourier 变换前后形式不变的信号——Gauss 型函数
g_{\alpha}\left( t \right) =\frac{1}{2\sqrt{\pi \alpha}}\exp \left\{ -\frac{t^2}{4\alpha} \right\}
不难发现
\begin{align}
\mathscr{F} \left\{ g_{\alpha}\left( t \right) \right\} &=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}{\frac{1}{2\sqrt{\pi \alpha}}\exp \left\{ -\frac{t^2}{4\alpha} \right\} \exp \left\{ -\mathrm{i}\omega t \right\} \mathrm{d}t}
\\
&=\frac{1}{\sqrt{2}\pi}\int_{-\infty}^{+\infty}{\exp \left\{ -\left( \frac{t}{2\sqrt{\alpha}}+\sqrt{\alpha}\mathrm{i}\omega \right) ^2-\alpha \omega ^2 \right\} \mathrm{d}\frac{t}{2\sqrt{\alpha}}}
\\
&=\frac{1}{\sqrt{2\pi}}\exp \left\{ -\alpha \omega ^2 \right\}
\end{align}
以此为窗进行的短时 Fourier 变换称为 Gabor 变换:
\begin{align}
\mathscr{F} \left\{ f\left( t \right) g_{\alpha}\left( t-b \right) \right\} &=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}{f\left( t \right) g_{\alpha}\left( t-b \right) \mathrm{e}^{-\mathrm{i}\omega t}\mathrm{d}t}
\\
&=\frac{1}{2\pi}\int_{-\infty}^{+\infty}{F\left( \xi \right) \mathrm{e}^{-\mathrm{i}\left( \omega -\xi \right) b}\mathrm{e}^{-\alpha \left( \omega -\xi \right) ^2}\mathrm{d}\xi}
\\
&=\frac{1}{2\sqrt{\pi \alpha}}\mathrm{e}^{-\mathrm{i}\omega b}\int_{-\infty}^{+\infty}{F\left( \xi \right) g_{\frac{1}{4\alpha}}\left( \xi -\omega \right) \mathrm{e}^{\mathrm{i}\xi b}\mathrm{d}\xi}
\end{align}
时域乘积在频域表现为卷积。 g_{\alpha}\left( t \right) 是时间窗函数, g_{\frac{1}{4\alpha}}(\xi) 则是相应的频率窗函数。时间窗宽度和频率窗宽度成反比。
1 Like
Thevenin
February 1, 2024, 12:17am
23
这学期本来打算修一门计算复杂性的课,结果第一节课没选上没听导致第二节课想试听但是完全听不懂遂退了
1 Like
Legendre
March 5, 2024, 6:27am
24
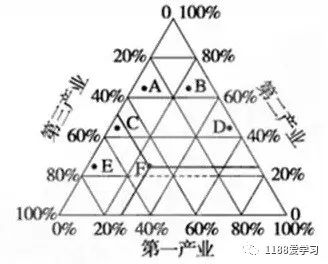
这里和水源同步更新吧(n-1) 维映射到 n 维。(0,255)的随机值,再给 G 生成(max(0,127-r),min(381-r,255)) 的随机值,最后得到 B,后来意识到这种方法生成的三个变量不满足同分布。如果按照三角坐标系的思路,为了让每个值的范围是 0~255,且平均值处于 127,其中一种方法是把上图正三角形挖去三个角,形成一个正六边形,然后在正六边形中均匀取点,得到三个对应的坐标,如下图。
当然在工程上还有更简单的处理方法,比如按最初方法生成完三个不同分布的随机数后随机交换位置,使之与 RGB 的对应关系也随机。如此同样可以实现最终的同分布。
原代码来自知乎文章
Python 画各种有趣的图及源码 。我改变了线条的长度、粗细和颜色。
代码
# -*- coding: utf-8 -*-
from turtle import *
import random
length = 10
angle = 90
setup(1280,720)
up()
goto(-640,-360)
down()
def draw_path(path):
for symbol in path:
if symbol == 'f':
colormode(255)
color(random.randint(0,255),random.randint(0,255),random.randint(0,255))
fd(length)
elif symbol == '+':
lt(angle)
elif symbol == '-':
rt(angle)
def apply_path(rules,path):
lit = [x for x in path]
for i in range(len(lit)):
symbol = lit[i]
if symbol == 'x':
lit[i] = rules[symbol]
elif symbol == 'y':
lit[i] = rules[symbol]
path = ''.join(lit)
return path
rules = {
'x':'+yf-xfx-fy+',
'y':'-xf+yfy+fx-'
}
path = 'x'
speed(0)
for i in range(7):
path = apply_path(rules,path)
draw_path(path)
done()
2 Likes
Legendre
March 5, 2024, 9:29am
25
如果函数 L:\mathbb{R}^n\to\mathbb{R} 满足如下条件:
\boldsymbol{v}\mapsto L(\boldsymbol{v}) 是凸函数 \displaystyle\lim_{|\boldsymbol{v}|\to \infty}\frac{L(\boldsymbol{v})}{|\boldsymbol{{v}}|}=\infty (超线性)
则 L 的 Legendre 变换为
L^*(\boldsymbol{p})=\sup_{\boldsymbol{v}\in\mathbb{R}^n}\{\boldsymbol{p}\cdot \boldsymbol{v}-L(\boldsymbol{v})\},\boldsymbol{p}\in\mathbb{R}^n.
Legendre 变换具有如下性质:
\boldsymbol{p}\mapsto L^*(\boldsymbol{p}) 是凸函数 \displaystyle\lim_{|\boldsymbol{p}|\to \infty}\frac{L^*(\boldsymbol{p})}{|\boldsymbol{p}|}=\infty (超线性) L^{**}=L
在理论力学中常见的 Legendre 变换是
L^*(\boldsymbol{p})=\boldsymbol{p}\cdot \boldsymbol{v}-L(\boldsymbol{v}),
其中
\boldsymbol{p}=\nabla L.
如果函数 L 可导,则两种定义是等价的。
1 Like
Legendre
July 3, 2024, 3:27am
28
基于 Markov 链的解决方法:
\left( \begin{matrix}
\frac{n-1}{n}& \frac{1}{n}& 0& \cdots\\
\frac{1}{n}& \frac{n-2}{n}& \frac{1}{n}& \cdots\\
0& \frac{1}{n}& \frac{n-2}{n}& \cdots\\
\cdots& \cdots& \cdots& \cdots\\
\end{matrix} \right)
根据 Basic Limit Theorem,显然存在均匀的稳态分布,所以分布会趋于均匀。因为加减同时进行,所以所有数的和不变。
使用 Minecraft 进行蒙特卡洛模拟
https://www.youtube.com/watch?v=LLss-7SPQ-oIf you are the original author or copyright holder of this video and want to remove this video for infringement or other reasons, please contact me via priva, 视频播放量 1122410、弹幕量 1260、点赞数 41317、投硬币枚数 1069、收藏人数...
2 Likes
Legendre
July 3, 2024, 3:28am
29
3 Likes
![]()