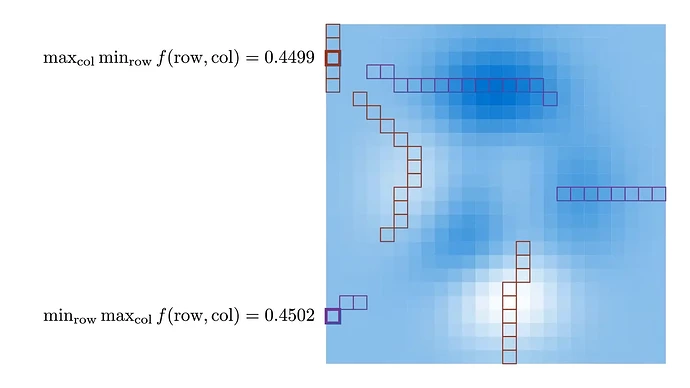
The max-min inequality
For any function
f: \mathcal{X} \times \mathcal{Y} \rightarrow \mathbb{R}:
max_{x \in \mathcal{X} } {min_{y \in \mathcal{Y} } {f(x, y)}} \le
min_{y \in \mathcal{Y} } {max_{x \in \mathcal{X} } {f(x, y)}}
好的里面挑差的总是比差的里面挑好的要好。